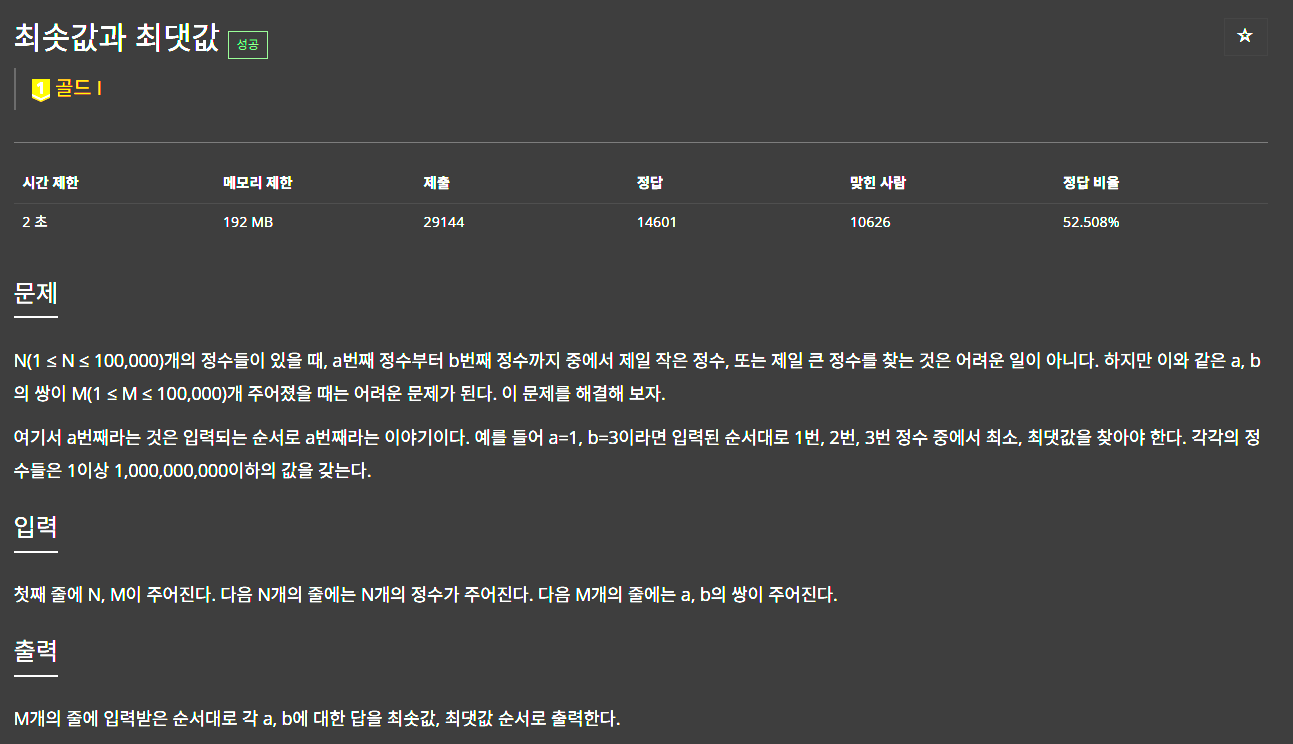
문제의 첫 줄을 읽자마자, 'a번째 정수부터 b번째 정수까지' 이 문구가 눈에 들어왔다. 이 말인 즉슨, 세그먼트 트리를 이용할 가능성이 매우 높다는 뜻. 그리고 뒤에를 읽었더니 최솟값과 최댓값을 구하라는 얘기가 보인다.
그리고 입력되는 수의 범위를 봤더니 N과 M이 모두 10^5 이하의 자연수라는 조건이 보였다. 즉, 만약 시간복잡도가 O(N)인 알고리즘을 써야한다면, 10^10번의 계산을 해야한단 의미였다.
이는 2초라는 시간 내에 절대적으로 불가하므로 처음 생각했던 세그먼트 트리의 개념을 이용해서 문제를 풀기로 했다.
그런데 약간의 고민이 생겼다. 최대와 최소 모두를 출력해야 하는데 어떻게 세그먼트 트리로 나타내지?
그래서 2개의 세그먼트 트리를 이용해 각각 특정 구간에서의 최대와 최소를 나타내는 트리로 만들기로 결심했다.
세그먼트 트리의 탐색 시간복잡도는 O(log N)이기에 가능한 얘기였다. 게다가 트리를 빌딩하는 것도 O(N)이지만 N이 10^5이하이기에 충분히 가능한 얘기였다.
이렇게 계획을 세운 나는 기존에 만들어뒀던 세그먼트 트리 클래스를 가져왔다.
class SegmentTree:
def __init__(self, n, data):
self.tree = [0] * 4 * n
self.data = data
def build(self, start, end, node):
if start == end:
self.tree[node] = self.data[start]
return self.tree[node]
mid = (start + end) // 2
self.tree[node] = self.build(start, mid, node * 2) + self.build(mid + 1, end, node * 2 + 1)
return self.tree[node]
def sum(self, start, end, node, left, right):
if left > end or right < start:
return 0
if left <= start and end <= right:
return self.tree[node]
mid = (start + end) // 2
return self.sum(start, mid, node * 2, left, right) + self.sum(mid + 1, end, node * 2 + 1, left, right)
def modify(self, start, end, node, index, NewValue):
if index < start or index > end:
return
if start == end:
self.tree[node] = NewValue
return
mid = (start + end) // 2
self.modify(start, mid, node * 2, index, NewValue)
self.modify(mid + 1, end, node * 2 + 1, index, NewValue)
self.tree[node] = self.tree[node * 2] + self.tree[node * 2 + 1]
하지만 이 클래스는 부분합을 나타내는 세그먼트 트리에 특정 노드의 수정을 해주는 modify까지 달려있어서 현재 문제와는 어울리지 않았다. 게다가 최대와 최소 트리를 만들기 위해 두 개의 개별적인 클래스를 만드는 것은 낭비라 생각해 기존 세그먼트 트리에서 modify를 제거하고 IsMin 매개변수를 추가로 넣어 이 트리가 최소에 대한 트리인지, 최대에 대한 트리인지 구분할 수 있도록 했다.
그렇게 만들어진 세그먼트 트리 코드는 다음과 같다.
class SegmentTree:
def __init__(self, n, data,isMin):
self.tree = [0] * 4 * n
self.data = data
self.isMin = isMin
def build(self, start, end, node):
if start == end:
self.tree[node] = self.data[start]
return self.tree[node]
mid = (start + end) // 2
if self.isMin:
self.tree[node] = min(self.build(start, mid, node * 2), self.build(mid + 1, end, node * 2 + 1))
else:
self.tree[node] = max(self.build(start, mid, node * 2), self.build(mid + 1, end, node * 2 + 1))
return self.tree[node]
def Return(self, start, end, node, left, right):
if left > end or right < start:
return float('inf') if self.isMin else -float('inf')
if left <= start and end <= right:
return self.tree[node]
mid = (start + end) // 2
ret = [ self.Return(start, mid, node * 2, left, right) ,self.Return(mid + 1, end, node * 2 + 1, left, right) ]
if self.isMin:
for i in range(2):
if ret[i] == 0: ret[i] = 10**6
return min(ret)
else:
for i in range(2):
if ret[i] == 0: ret[i] = -1
return max(ret)
그리고 여기에 문제 조건에 맞는 여러 살을 붙여 나는 문제를 풀어낼 수 있었다.

class SegmentTree:
def __init__(self, n, data,isMin):
self.tree = [0] * 4 * n
self.data = data
self.isMin = isMin
def build(self, start, end, node):
if start == end:
self.tree[node] = self.data[start]
return self.tree[node]
mid = (start + end) // 2
if self.isMin:
self.tree[node] = min(self.build(start, mid, node * 2), self.build(mid + 1, end, node * 2 + 1))
else:
self.tree[node] = max(self.build(start, mid, node * 2), self.build(mid + 1, end, node * 2 + 1))
return self.tree[node]
def Return(self, start, end, node, left, right):
if left > end or right < start:
return float('inf') if self.isMin else -float('inf')
if left <= start and end <= right:
return self.tree[node]
mid = (start + end) // 2
ret = [ self.Return(start, mid, node * 2, left, right) ,self.Return(mid + 1, end, node * 2 + 1, left, right) ]
if self.isMin:
for i in range(2):
if ret[i] == 0: ret[i] = 10**6
return min(ret)
else:
for i in range(2):
if ret[i] == 0: ret[i] = -1
return max(ret)
N,M = map(int,input().split())
lst = []
for _ in range(N):
lst.append(int(input()))
minSegmentTree = SegmentTree(N,lst,True)
minSegmentTree.build(0,N-1,1)
maxSegmentTree = SegmentTree(N,lst,False)
maxSegmentTree.build(0,N-1,1)
for _ in range(M):
a,b = map(int,input().split())
print(minSegmentTree.Return(0,N-1,1,a-1,b-1),maxSegmentTree.Return(0,N-1,1,a-1,b-1))
'백준' 카테고리의 다른 글
| BOJ 17633 제곱수의 합 (More Huge) (0) | 2025.04.22 |
|---|---|
| BOJ 1786 찾기 (0) | 2025.04.03 |
| BOJ 1708 볼록 껍질 (0) | 2025.04.01 |
| BOJ 13926 gcd(n, k) = 1 (0) | 2025.03.31 |